Definición de un Grafo y Notación

Definición de un Grafo y Notación

Según las ideas introductorias que se tienen sobre los grafos, estos deben tener al menos dos componentes: por una parte vértices o nodos, y por otra parte aristas o líneas que conecten esos vértices. Por lo tanto podemos considerar que un grafo es la relación entre dos conjuntos diferentes, la relación entre un conjunto de nodos y un conjunto de vértices. Pero, es necesario formalizar estos hechos. 

Supongamos que tenemos un conjunto de vértices, al cual llamaremos V, supongamos que al conjunto de aristas lo llamamos E. Ahora las preguntas fundamentales son ¿de qué forma serán los elementos de V? y ¿de qué forma serán los elementos de E?

Contestemos la primera pregunta, como V esta´ formado por vértices y a su vez, los vértices los podemos representar por puntos, es decir, por letras (a,b,c,...,A,B,C,...), por números (0,1,2,...) o incluso por símbolos de diferente índole. Entonces los elementos que componen al conjunto V, pueden ser letras, números o símbolos.

Hasta aquí no hay mucho problema ¿verdad? La cuestión ahora, es definir los elementos que componen al conjunto E. Se sabe, que el conjunto E, está formado por aristas, pero ¿cómo se pueden representar las aristas en nomenclatura matemática? las aristas están determinadas por dos puntos, es decir por dos vértices, por la tanto esa arista la podemos representar mediante un par no necesariamente ordenado (B, D), que va indicar que justamente hay una arista conectando esos dos vértices o nodos. Por lo cual, se puede inferir que el conjunto E, en realidad, esta´ formado por pares no ordenados (ya que también podría ser válido representar esa arista como (D, B), con lo cual pierde la idea de orden). Formalmente se define un grafo de la siguiente manera:

Definición 1.2.1.1 Un grafo G es una dupla G = (V, E), donde V es un conjunto finito de vértices o nodos y E es un conjunto de pares no necesariamente ordenados de vértices, denotados por (x, y), que se denominan lados, aristas, etc.

A partir de ´esta Definición, vamos adoptar alguna notación básica que sirva de referencia para tratar aspectos generales de los grafos. Por ejemplo, si (x, y) es una arista de grafo, al vértice x le llamaremos vértice de entrada o inicial y al vértice y le llamaremos vértice de salida o terminal.

Denotamos por ν (G) y ε (G) el número de vértices y el número de aristas de G respectivamente. Puesto que E es un conjunto de pares, es posible que existen pares repetidos, en este caso el grafo G tiene lados múltiples. También es posible que algún par no ordenado de E tenga el mismo vértice repetido (es decir que la arista parta de un punto y llegue al mismo punto), en este caso decimos que el lado es un lazo (loop) o bucle.

Generalmente, cuando hablamos de un grafo, nos imaginamos directamente un dibujo como la figura

Pero, resulta difícil hacer algoritmos sobre dibujos, por lo cual, es necesario representar el grafo mediante simbología matemática.

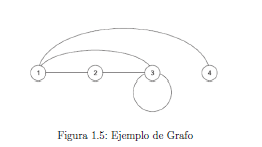
De ´esta manera, podemos representar el grafo de la figura 1.5 como:

G = (V, E); 

V = {1, 2, 3, 4} 

E = {(1,2), (1,3), (1,4), (2,3), (3,3)}

Además:

ν(G) = 4

ε(G) = 5

Observe también, que existe un lazo o bucle dentro del grafo, ya que existe una arista que parte del vértice 3 y llega al vértice 3, es justamente la arista (3,3). Además, si observamos con detenimiento, el conjunto de aristas, también puede representarse mediante E = {(2,1), (3,1), (4,1), (3,2), (3,3)}. Por esta razón, es que se define el conjunto de E de un grafo como un conjunto de pares no necesariamente ordenados, ya que el orden no nos interesa mucho en ´este punto.

En teoría de grafos, sólo queda lo esencial del dibujo: la forma de las aristas no son relevantes, sólo importa a qué vértices están unidas. La posición de los vértices tampoco importa, y se puede variar para obtener un grafo más claro. Bajo este análisis, los grafos de la figura 1.6, son equivalentes, ya que ambos tendrán la misma representación matemática (comprobarlo) independientemente de su forma. Cuando dos grafos son equivalentes, les llamaremos isomorfos.